Volume of space enclosed by sphere and paraboloid using spherical coordinates???

This seems trivial if you understand triple integration and simple coordinate systems; however, a question of this type made me think for a moment since its not as simple as converting from cylindrical to spherical coordinates or setting up bounds (Ρ, Φ , θ). The solution isn’t as complex as you would imagine. Similar to many other problems, seeing the solution will make you say, “ahh okay.” Lets see what we are tackling.
We have a sphere with radius sqrt(2):

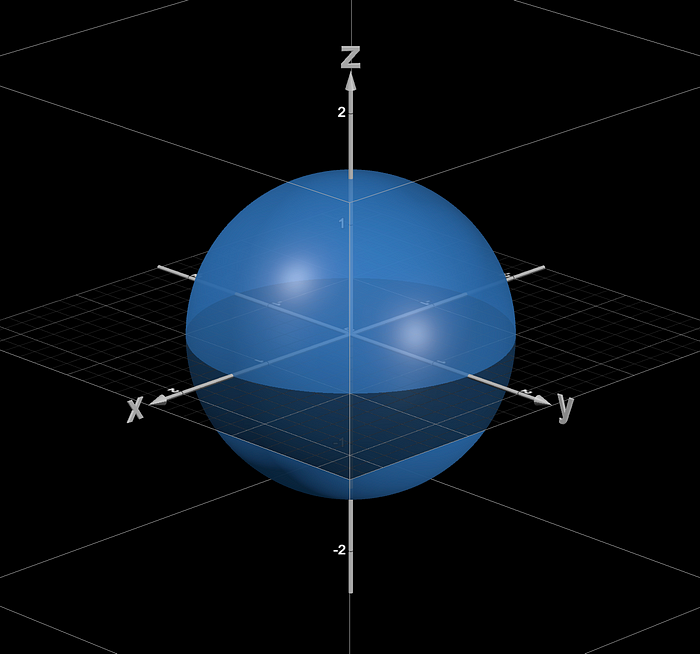
And a regular paraboloid:


The volume we are attempting to find is the following rotated by 2π on the z axis. I have presented these bound in the xy plane:


Cylindrical Coordinates
The simple solution is using the cylindrical coordinate system ( r, θ, z ). To refresh your mind, we can transform from rectangular coordinates (x,y,z) to coordinates by doing the following conversions:

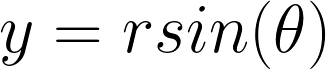

By definition we can also derive the following:
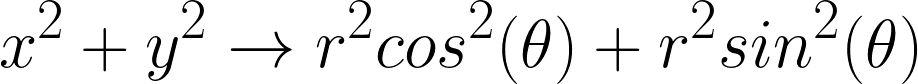


Lets also review how the cylindrical coordinate system looks. r is the projection of the hypotenuse that connects the target point to origin

To set up our triple itegration ( to find volumn of space ) we must find bounds D using our coordinate system. We use the following bounds
Our θ will be the rotation of the shape around the z axis

Our r will be the the radius of the projection of the our shape at any xy slice. We say one since that is the intersection of both shapes

Our z will be the min and max value of z defined by our shapes ( sphere and paraboloid).

Then our bound D is
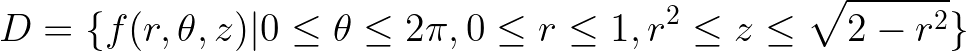
We can use the bounds D to set up our triple integral using the

Then we solve this integration:

Spherical Coordinates
The less obvious solution is using spherical coordinates (Ρ, Φ , θ), where Ρ is the length of the line connecting origin to target point, Φ is the angle from positive z axis to Ρ, and θ is the rotation of the shape around z axis.

we can transform from cylindrical to spherical using the following:

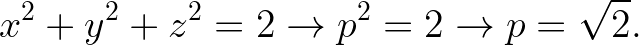
If we try to set up our bounds like we did last time we will quickly see that our integration results do not match. This has to do with the curvature that the paraboloid presents to the bottom of the shape. The best work around is to divide our shape into 2 subregions as follows, integrate separately and then add:


The two bounds are the following:


Then we set up our triple integrals and solve:


The sum of solutions give us the correct result.

I hope you guys enjoyed this little piece and found some use. I purposfully didn’t show all steps … practice practice practice.
